编译原理作业4

Exercise 4.1

Given the following grammar ：
$$
S → ( L ) | a\
L → L , S | S
$$

• Eliminate left recursions in the grammar.

• Draw the transition diagrams for the grammar.

• Write a recursive descent predictive parser.

• Indicate the procedure call sequence for an input sentence (a, (a, a)).

首先消除左递归后结果如下：
$$
S → ( L ) | a\
L → SL’\
L’ → ,SL’ | \epsilon
$$
画出transition diagrams，如下：

对transition diagrams做reduce： 所以最终的结果如下：

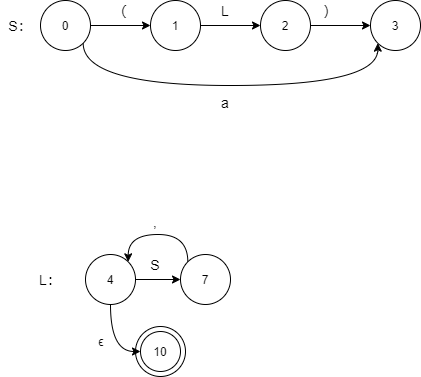
recursive descent predictive parser如下：

void S() throws SyntacticException {
    if (lookahead.equals(new Token('('))) {
    	match(new Token('('));
    	L();
    	match(new Token(')'));
    } else if (lookahead.equals(new Token('a'))) {
    	match(new Token('a'));
    } else {
    	throw new SyntacticException();
    }
}
void L() throws SyntacticException {
    S();
    while (lookahead.equals(new Token(','))) {
        match(new Token(','));
        S();
    }
}

对于(a, (a, a))，运行如下：

在这里用缩进代表函数调用的层数，运行如下：

call S():
	match '(';
	call L():
		call S():
			match 'a';
			return;
		match ',';
		call S():
			match '(';
			call L():
				call S():
					match 'a';
					return;
				match ','
				call S():
					match 'a';
					return;
				return;
			match ')';
			return;
		return;
	match ')';
	return;
	

Exercise 4.2

Consider the context-free grammar

$$
S → a \ S\ b\ S\ |\ b\ S\ a\ S\ |\ \epsilon
$$

Can you construct a predictive parser for the grammar? and why?

不可以，理由如下：

令$\alpha = a \ S\ b\ S\ |\ b\ S\ a\ S\ $,$\beta = \epsilon$,有$S → \alpha \ |\ \beta $

可以得到：

$FIRST(\alpha) = {a,b}$,$FOLLOW(S) = {a,b, \psi}$

所以有：

$FIRST(\alpha)\ \cap \ FOLLOW(S) \neq \varnothing$

所以无法给该语法构建一个可预测的parser。

Exercise 4.3

Compute the FIRST and FOLLOW for the start symbol of the following grammar.
$$
S → \ S\ S\ +\ |\ S\ S\ *\ |\ a
$$
$FIRST(S) = {a}$

$FOLLOW(S) = {+, * , \psi}$